RG of Polyhedra (Examples)

Calculation of the Radius of Gyration (Rg) of the Truncated Icosahedron, Cuboctahedron, Rhombicuboctahedron, Octahedron and of their variations.

As an example, the Radius of Gyration (Rg) of a Truncated Icosahedron (the shape of the C60-molecule) is being calculated. The polyhedral shape consists of 20 hexagons and 12 pentagons (60 vertices, 32 faces, 90 edges) with an unilateral edge-length a (here we take unit length = 1). All parameters for the calculation of Rg, such as out-, mid- and in-sphere radii (ro, rm, ri), respectively, can be found at Wolfram MathWorld or at Visual Polyhedra.

An animation of the Truncated Icosahedron can be visualized here.

The parameters for the solid shape are entered as input into the Rg-calculator as shown below:

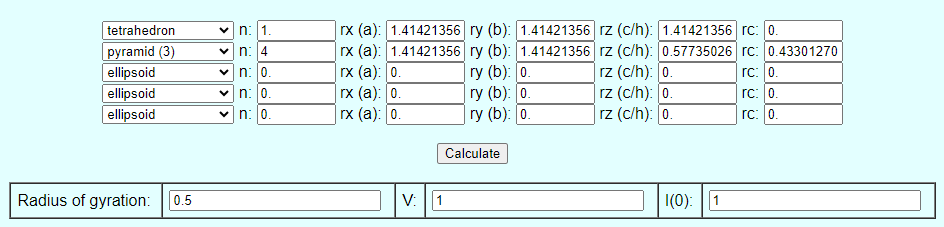
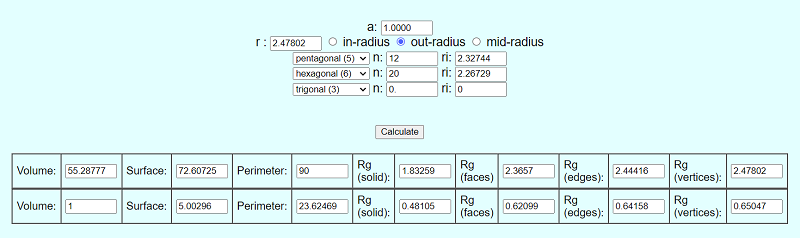
Parameter (Truncated Icosahedron)	Value
Volume	55.288
Surface	72.607
Perimeter	90.000
out-sphere radius ro	2.478
mid-sphere radius rm	2.427
in-sphere radius ri (pentagons)	2.327
in-sphere radius ri (hexagons)	2.267
Rg of solid	1.833
Rg of faces	2.366
Rg of edges	2.444
Rg of vertices ( = ro)	2.478

Table 1. Shape parameters and calculated values for Rg (rounded) of the regular truncated icosahedron (C60) of unit length a=1 ( = edge length). Rg scales linearly with the edge-length a. Units are arbitrary.

As another example, the Radius of Gyration (Rg) of the Cuboctahedron (CO) and of two of its variations (Octahemioctahedron (OH) and Cubohemioctahedron (CH)) are being calculated. The polyhedral shape consists of 8 trigons and 6 tetragons (12 vertices, 14 faces, 24 edges) with an unilateral edge-length a (here we take unit length = 1). All parameters for the calculation of Rg, such as out-, mid- and in-sphere radii (ro, rm, ri), respectively, can be found at Wolfram MathWorld or at Visual Polyhedra.

An animation of the Cuboctahedron can be visualized here.

The parameters for the solid shape are entered as input into the Rg-calculator as shown below:

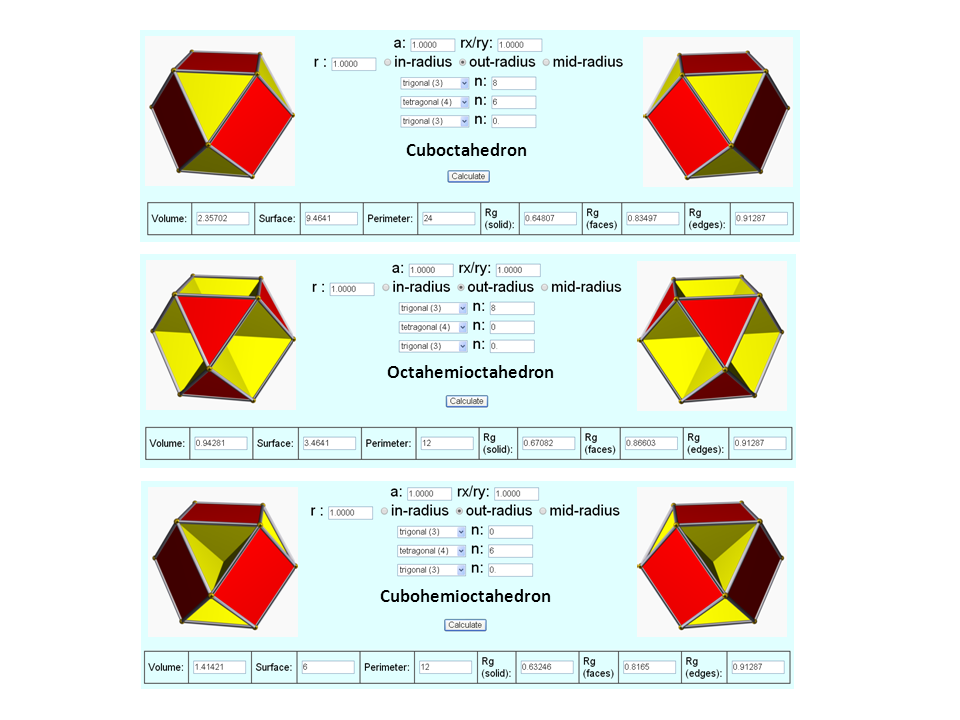
Parameter (Cuboctahedron)	Value
Volume	2.357
Surface	9.464
Perimeter	24.000
out-sphere radius ro	1.000
mid-sphere radius rm	0.866
in-sphere radius ri (trigons)	0.816
in-sphere radius ri (tetragons)	0.707
Rg (CO)	0.648
Rg (OH)	0.671
Rg (CH)	0.632

Table 2. Shape parameters and calculated values for Rg (rounded) of the Cuboctahedron and of two variations with unit length a=1 ( = edge length). Rg scales linearly with the edge-length a. Units are arbitrary.

Next, the Radius of Gyration (Rg) of the Small Rhombicuboctahedron (RCO) and of two of its variations (Small Cubicuboctahedron (CCO) and Small Rhombihexahedron (RH)) are being calculated. The polyhedral shape consists of 8 trigons and 18 tetragons (24 vertices, 26 faces, 48 edges) with an unilateral edge-length a (here we take unit length = 1). All parameters for the calculation of Rg, such as out-, mid- and in-sphere radii (ro, rm, ri), respectively, can be found at Wolfram MathWorld or at Visual Polyhedra.

An animation of the Rhombicuboctahedron can be visualized here.

The parameters for the solid shape are entered as input into the Rg-calculator as shown below:

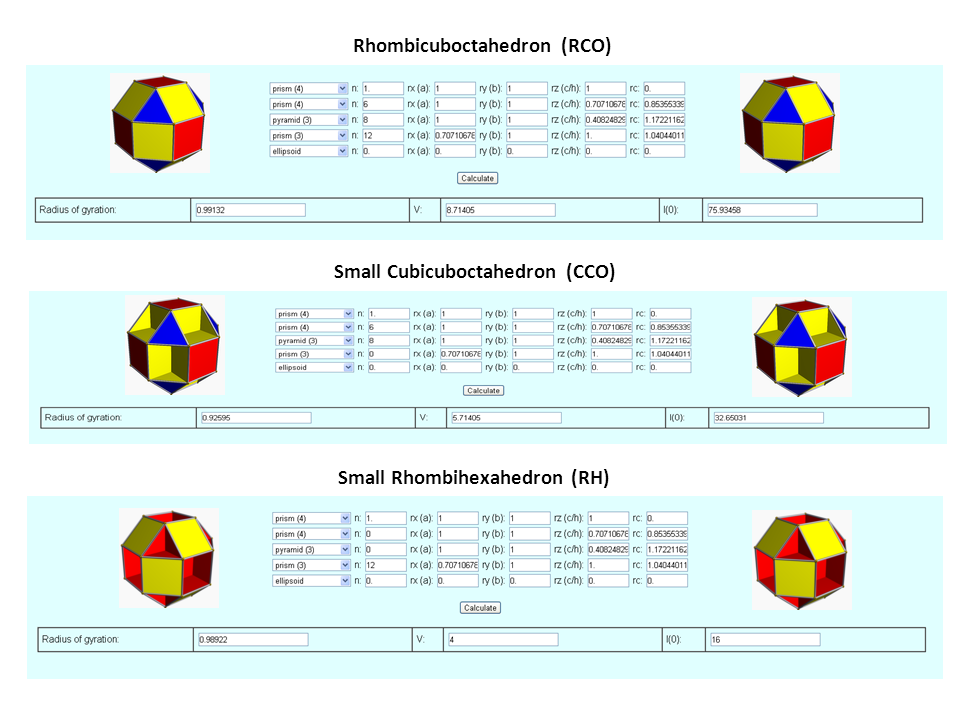
Parameter (Small Rhombicuboctahedron)	Value
Volume	8.714
Surface	21.464
Perimeter	48.000
out-sphere radius ro	1.399
mid-sphere radius rm	1.307
in-sphere radius ri (trigons)	1.274
in-sphere radius ri (tetragons)	1.207
Rg (RCO)	0.991
Rg (CCO)	0.926
Rg (RH)	0.989

Table 3. Shape parameters and calculated values for Rg (rounded) of the Samll Rhombicuboctahedron and of two variations with unit length a=1 ( = edge length). Rg scales linearly with the edge-length a. Units are arbitrary.

Last, the Radius of Gyration (Rg) of two variations of the Octahedron (Stella Octangula (SO) and Tetrahemihexahedron (THH)) are being calculated. The polyhedral shape (octahedron) consists of 8 trigons (6 vertices, 8 faces, 12 edges) with an unilateral edge-length a (here we take unit length = 1). In case of the Stalla Octangula all eight faces are stellated with tetrahedra of edge lengths equal to a, in case of the Tetrahemihexahedron four faces are removed (4 of the 8 trigonal pyramids are 'cut out'). In both cases the position of the centroid remains the same.

The parameters for the solid shape are entered as input into the Rg-calculator (and also here) as shown below:

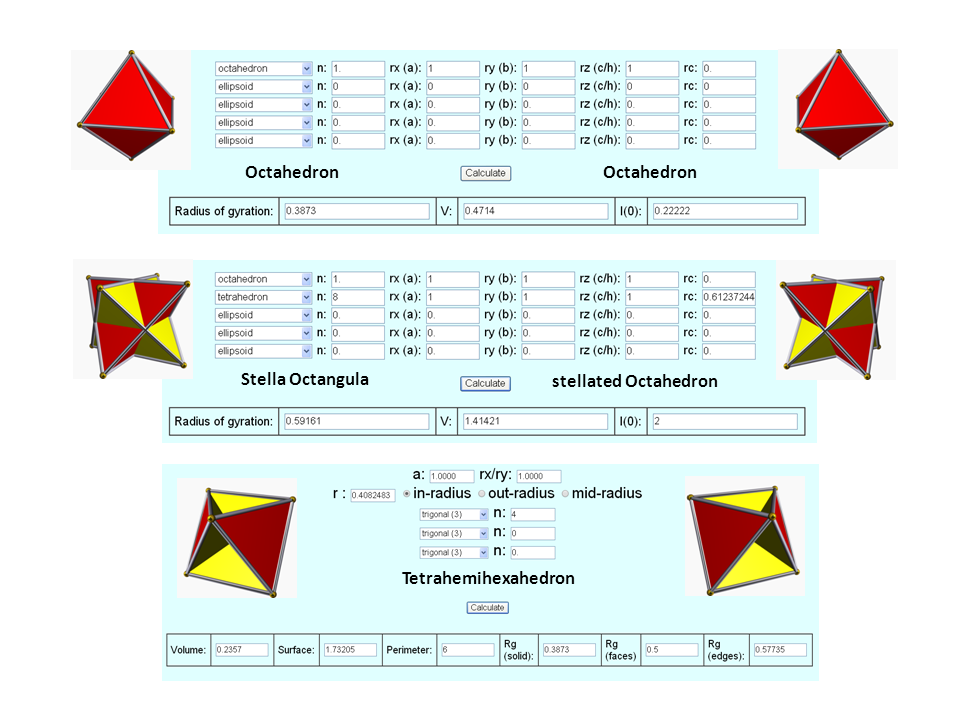
Parameter (Octahedron)	Value
Volume	0.471
Surface	3.464
Perimeter	12.000
out-sphere radius ro	0.707
mid-sphere radius rm	0.500
in-sphere radius ri (trigons)	0.408
Rg (O)	0.387
Rg (SO)	0.592
Rg (THH)	0.387

Table 3. Shape parameters and calculated values for Rg (rounded) of the Octahedron and of two variations with unit length a=1 ( = edge length). Note, Rg of the THH is the same as for the Octahedron, no matter how many trigonal pyramids are removed from the Octahedron (provided the location of the centroid remains the same). Rg scales linearly with the edge-length a. Units are arbitrary.

A cube of edge length = 1 can be dissected into a central regular tetrahedron with edge length = √2 (rx=ry=rz) and 4 attached trigonal pyramids with edge length √2 (of the trigonal base, rx=ry) and height = 1/√3 (rz) attached to the 4 faces of the central tetrahedron. The distance between the center of mass of the tetrahedron to each center of mass of the 4 pyramids is √3/4 (rc). Calculation the Radius of Gyration of this cube (with edge length = 1) from these 5 subunits (with the proper geometry and coordinates) results in Rg=0.5 and V=1, (Rg(cube) = ∛V/2), using the Rg-calculator as shown below:

Alternatively a cube of edge length = 1 can also be dissected into 6 quadratic pyramids with edge length = 1 (of the quadratic base, rx=ry) and height = 1/2 (rz). The distance between the center of mass of the cube to each center of mass of the 6 pyramids is 3/8 (rc). Calculation the Radius of Gyration of this cube (with edge length = 1) from these 6 subunits (with the proper geometry and coordinates) results in Rg=0.5 and V=1, (Rg(cube) = ∛V/2), using the Rg-calculator as shown below:

Author: M.Kriechbaum, TU-Graz (2013), e-mail: manfred.kriechbaum@tugraz.at