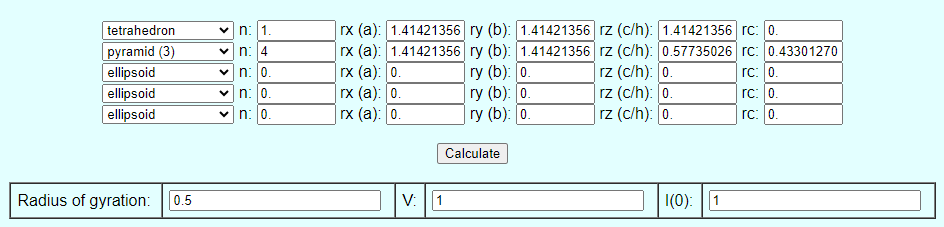

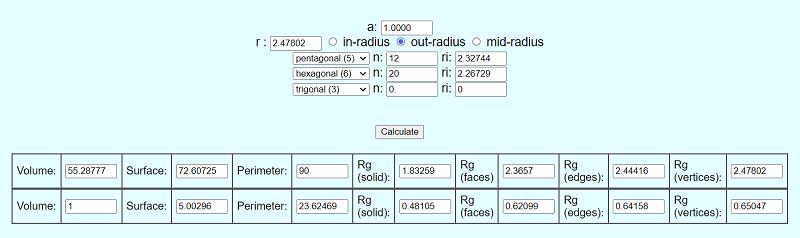
| Parameter (Truncated Icosahedron) | Value |
| Volume | 55.288 |
| Surface | 72.607 |
| Perimeter | 90.000 |
| out-sphere radius ro | 2.478 |
| mid-sphere radius rm | 2.427 |
| in-sphere radius ri (pentagons) | 2.327 |
| in-sphere radius ri (hexagons) | 2.267 |
| Rg of solid | 1.833 |
| Rg of faces | 2.366 |
| Rg of edges | 2.444 |
| Rg of vertices ( = ro) | 2.478 |
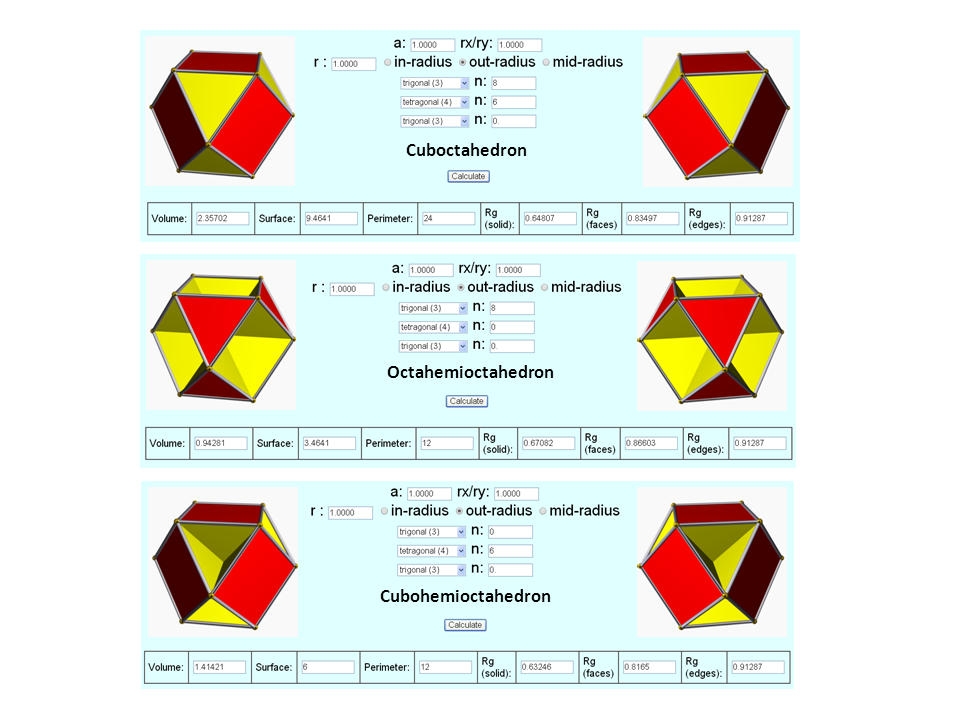
| Parameter (Cuboctahedron) | Value |
| Volume | 2.357 |
| Surface | 9.464 |
| Perimeter | 24.000 |
| out-sphere radius ro | 1.000 |
| mid-sphere radius rm | 0.866 |
| in-sphere radius ri (trigons) | 0.816 |
| in-sphere radius ri (tetragons) | 0.707 |
| Rg (CO) | 0.648 |
| Rg (OH) | 0.671 |
| Rg (CH) | 0.632 |
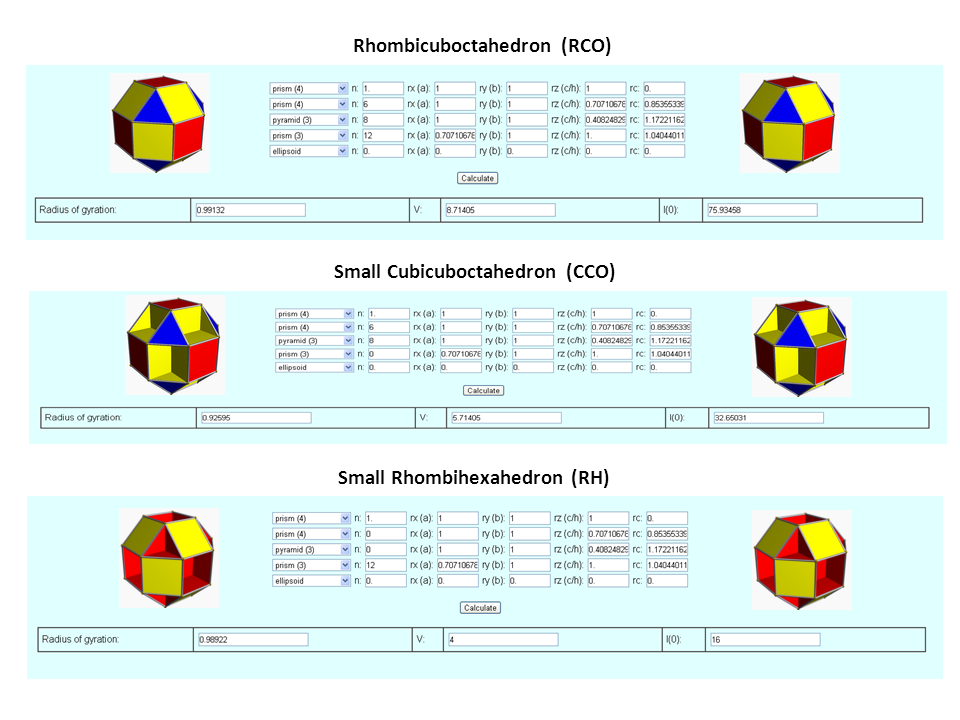
| Parameter (Small Rhombicuboctahedron) | Value |
| Volume | 8.714 |
| Surface | 21.464 |
| Perimeter | 48.000 |
| out-sphere radius ro | 1.399 |
| mid-sphere radius rm | 1.307 |
| in-sphere radius ri (trigons) | 1.274 |
| in-sphere radius ri (tetragons) | 1.207 |
| Rg (RCO) | 0.991 |
| Rg (CCO) | 0.926 |
| Rg (RH) | 0.989 |
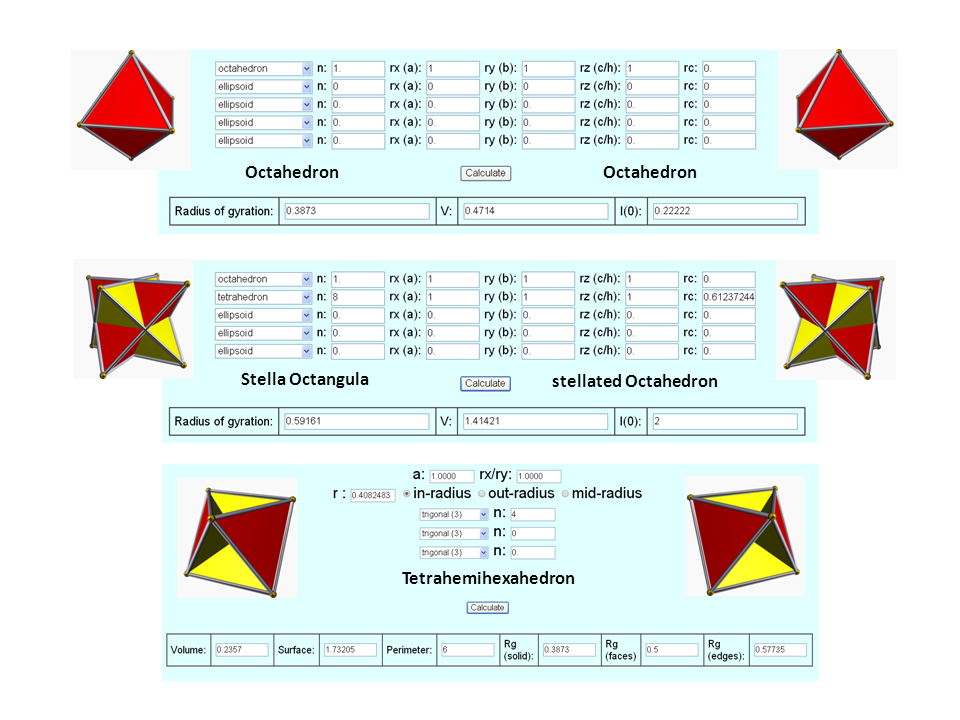
| Parameter (Octahedron) | Value |
| Volume | 0.471 |
| Surface | 3.464 |
| Perimeter | 12.000 |
| out-sphere radius ro | 0.707 |
| mid-sphere radius rm | 0.500 |
| in-sphere radius ri (trigons) | 0.408 |
| Rg (O) | 0.387 |
| Rg (SO) | 0.592 |
| Rg (THH) | 0.387 |