Cubic Space Groups from 195-230


The following tables list all 36 possible crystallographic cubic space groups (from 195 to 230), their respective symmetry and in brackets to which of the 17 possible aspects they belong.

195. P 2 3 (1) 196. F 2 3 (13) 197. I 2 3 (8) 198. P 21 3 (2) 199. I 21 3 (8) 200. P m -3 (1)
201. P n -3 (4) 202. F m -3 (13) 203. F d -3 (15) 204. I m -3 (8) 205. P a -3 (7) 206. I a -3 (10)
207. P 4 3 2 (1) 208. P 42 3 2 (2) 209. F 4 3 2 (13) 210. F 41 3 2 (14) 211. I 4 3 2 (8) 212. P 43 3 2 (3)
213. P 41 3 2 (3) 214. I 41 3 2 (9) 215. P -4 3 m (1) 216. F -4 3 m (13) 217. I -4 3 m (8) 218. P -4 3 n (5)
219. F -4 3 c (16) 220. I -4 3 d (11) 221. P m -3 m (1) 222. P n -3 n (6) 223. P m -3 n (5) 224. P n -3 m (4)
225. F m -3 m (13) 226. F m -3 c (16) 227. F d -3 m (15) 228. F d -3 c (17) 229. I m -3 m (8) 230. I a -3 d (12)
       

01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17
195 198 212 201 218 222 205 197 214 206 220 230 196 210 203 219 228
200 208 213 224 223 --- --- 199 --- --- --- --- 202 --- 227 226 ---
207 --- --- --- --- --- --- 204 --- --- --- --- 209 --- --- --- ---
215 --- --- --- --- --- --- 211 --- --- --- --- 216 --- --- --- ---
221 --- --- --- --- --- --- 217 --- --- --- --- 225 --- --- --- ---
--- --- --- --- --- --- --- 229 --- --- --- --- --- --- --- --- ---

Reference: J.S.Kasper and K.Lonsdale, Eds (1967), in: International Tables for X-Ray Crystallography, Vol 2, page 147 (Table 3.8.6B)


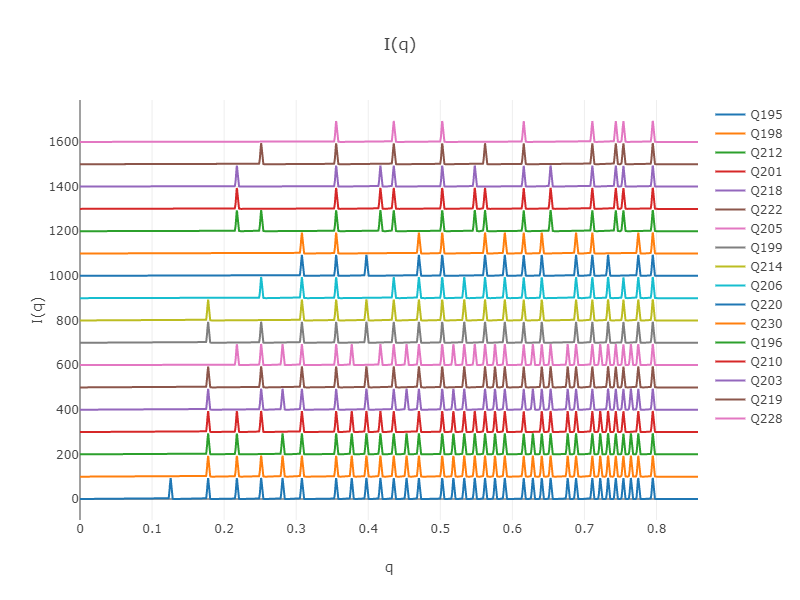
The following plot shows all possible (different) 17 XRD-patterns of the cubic space groups from 195 to 230 (see table above) up to n = h*h + k*k + l*l = 40. Lattice spacing is 50 units. Created by the XRD pattern simulator for cubic lattices.



Author: Manfred Kriechbaum Manfred.Kriechbaum@tugraz.at (2002, 2025)